Tout le monde connaît le théorème de Pythagore, qui permet de calculer la longueur des côtés d'un triangle rectangle grâce à la formule \(c^2 = b^2+a^2\) où \(c\) est l'hypoténuse du triangle. Cette formule s'avère alors très pratique pour résoudre de nombreux problèmes géométriques. Cependant, qu'en est-il pour les triangles non rectangles ? Existe-t-il un théorème pour calculer la longueur de leurs côtés ? Oui : le théorème d'Al-Kashi, que l'on voit, en général, quelques années après Pythagore, une fois que vecteurs et produits scalaires commencent à être maîtrisés.

Formulation du théorème d'Al-Kashi

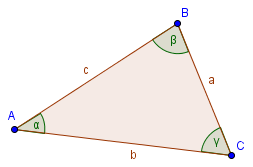
Soit un triangle ABC quelconque où l'on note \(a = BC\), \(b = CA\), \(c = AB\) et les angles \(\alpha\) en A, \(\beta\) en B, \(\gamma\) en C.
Alors, on a les 3 égalités suivantes :

$$\begin{cases} a^2 = c^2 + b^2 - 2 \cdot c \cdot b \cdot cos(\alpha) \\b^2 = c^2 + a^2 - 2 \cdot c \cdot a \cdot cos(\beta) \\c^2 = b^2 + a^2 - 2 \cdot b \cdot a \cdot cos(\gamma) \end{cases}$$

Démonstration du théorème d'Al-Kashi

Tout d'abord, rappelons que :

• Un vecteur \(\vec{AB}\) correspond au déplacement du point A au point B : il a donc une direction, un sens et une norme \(||\vec{AB}||\)
• Le produit scalaire de 2 vecteurs peut être calculer de la manière suivante :
  \(\vec{u}.\vec{v} = ||\vec{u}|| \cdot ||\vec{v}|| \cdot cos(\vec{u}, \vec{v})\)

Rappelons aussi que, pour un vecteur \(\vec(AB)\) quelconque :

$$\vec(AB)^2 = AB \cdot AB \cdot cos(\vec(AB), \vec(AB)) = AB^2$$

Maintenant, passons à la démonstration. Plaçons-nous dans un triangle quelconque ABC et partons de \(BC^2\) pour obtenir les égalités suivantes :

$$\begin{align} BC^2 &= \vec{BC}^2 = (\vec{BA} + \vec{AC})^2 \\ &= \vec{BA}^2 + \vec{AC}^2 + 2\vec{BA}.\vec{AC} \\ &= BA^2 + AC^2 + 2 \cdot BA \cdot AC \cdot cos(\vec{BA}, \vec{AC}) \end{align}$$Comme \(cos(\vec{BA}, \vec{AC}) = cos(-\vec{AB}, \vec{AC}) = -cos(\vec{AB}, \vec{AC})\), on obtient :

$$BC^2 = BA^2 + AC^2 - 2.BA.AC.cos(\vec{AB}, \vec{AC})$$

Et en utilisant les notations spécifiées précédemment, on obtient bien :

$$a^2 = c^2+b^2 - 2 \cdot c \cdot b \cdot cos(\alpha)$$

Il est alors maintenant possible de répéter le raisonnement vu plus haut en partant, cette fois-ci, de \(AB^2\), puis de \(CA^2\) pour obtenir les égalités restantes :

$$AB^2 = AC^2 + CB^2 - 2.AC.CB.cos(\vec{AC}, \vec{CB})$$$$CA^2 = CB^2 + BA^2 - 2.CB.BA.cos(\vec{CB}, \vec{BA})$$

Vous venez donc de découvrir les 3 égalités du théorème d'Al-Kashi ainsi que leur démonstration.

Remarque

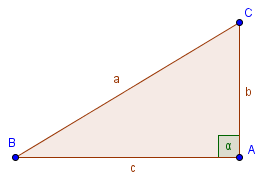
Essayons d'appliquer le théorème d'Al-Kashi à un triangle rectangle pour voir si la formule du théorème de Pythagore est obtenue.

Plaçons nous dans un triangle ABC rectangle en A en utilisant encore les mêmes notations et calculons la longueur \(a\) avec la formule trouvée précédemment :

$$a^2 = c^2 + b^2 - 2 \cdot c \cdot b \cdot cos(\alpha)$$Comme ABC est rectangle en A, \((\vec{AB}, \vec{AC}) = \alpha = 90^{\circ}\), donc \(cos(\alpha) = 0\), ce qui nous donne l'égalité suivante :

$$a^2 = c^2 + b^2$$Nous retombons heureusement bien sur la formule donnée par le théorème de Pythagore ! Le théorème d'Al-Kashi n'est alors ni plus ni moins qu'une généralisation de ce dernier.